Turbidity in wetlands

• Products used: ls8_sr, ls9_sr, wofs_ls

**Keywords**: :index:`data used; landsat 9`, :index:`data used; landsat 8`, :index:`data used; WOfS`, :index:`NDTI`, :index:`wetlands`

Background

In this notebook, we calculate turbidity in wetland areas through the Normalised Difference Turbidity Index (NDTI). Turbidity refers to the optical clarity of the water. While it is not strictly correlated with suspended matter, chlorophyll content, or other metrics, it is often used in conjunction to provide a more holistic analysis of water quality.

NDTI is a band index defined as:

\(\text{NDTI} = \frac{\text{Red} - \text{Green}}{\text{Red} + \text{Green}}\)

Lacaux et al, 2007

Here, we investigate NDTI over wetland areas in a several-year time series, through both a seasonal animation and a time series plot.

Description

1. Load packages and connect to the datacube

2. Define area of interest and time range

3. Mask areas with water using WOfS

4. Plot and animate

5. Investigate wetlands extent over time

---

Getting started

To run this analysis, run all the cells in the notebook, starting with the “Load packages” cell.

Load packages

%matplotlib inline

# Force GeoPandas to use Shapely instead of PyGEOS
# In a future release, GeoPandas will switch to using Shapely by default.
import os
os.environ['USE_PYGEOS'] = '0'

import datacube
import numpy as np
import xarray as xr
import geopandas as gpd
import matplotlib.pyplot as plt
import rioxarray
from IPython.display import Image
from geopandas import GeoDataFrame
from datacube.utils.geometry import Geometry

from deafrica_tools.plotting import display_map, rgb, xr_animation, map_shapefile
from deafrica_tools.spatial import xr_vectorize, xr_rasterize
from deafrica_tools.datahandling import load_ard, mostcommon_crs, wofs_fuser
from deafrica_tools.bandindices import calculate_indices
from deafrica_tools.areaofinterest import define_area

Connect to the datacube

dc = datacube.Datacube(app="Wetland_turbidity")

Define area of interest

To define the area of interest, there are two methods available:

1. By specifying the latitude, longitude, and buffer. This method requires you to input the central latitude, central longitude, and the buffer value in square degrees around the center point you want to analyze. For example, lat = 10.338, lon = -1.055, and buffer = 0.1 will select an area with a radius of 0.1 square degrees around the point with coordinates (10.338, -1.055).

   Alternatively, you can provide separate buffer values for latitude and longitude for a rectangular area. For example, lat = 10.338, lon = -1.055, and lat_buffer = 0.1 andlon_buffer = 0.08 will select a rectangular area extending 0.1 degrees north and south, and 0.08 degrees east and west from the point (10.338, -1.055).

   For reasonable loading times, set the buffer as 0.1 or lower.

2. By uploading a polygon as a GeoJSON or Esri Shapefile. If you choose this option, you will need to upload the geojson or ESRI shapefile into the Sandbox using Upload Files button in the top left corner of the Jupyter Notebook interface. ESRI shapefiles must be uploaded with all the related files (.cpg, .dbf, .shp, .shx). Once uploaded, you can use the shapefile or geojson to define the area of interest. Remember to update the code to call the file you have uploaded.

To use one of these methods, you can uncomment the relevant line of code and comment out the other one. To comment out a line, add the "#" symbol before the code you want to comment out. By default, the first option which defines the location using latitude, longitude, and buffer is being used.

If running the notebook for the first time, keep the default settings below. This will demonstrate how the analysis works and provide meaningful results.

# Method 1: Specify the latitude, longitude, and buffer
aoi = define_area(lat=13.83408, lon=-16.56464 , lat_buffer =0.2025, lon_buffer = 0.1025)

# Method 2: Use a polygon as a GeoJSON or Esri Shapefile.
#aoi = define_area(vector_path='aoi.shp')

#Create a geopolygon and geodataframe of the area of interest
geopolygon = Geometry(aoi["features"][0]["geometry"], crs="epsg:4326")
geopolygon_gdf = gpd.GeoDataFrame(geometry=[geopolygon], crs=geopolygon.crs)

# Get the latitude and longitude range of the geopolygon
lat_range = (geopolygon_gdf.total_bounds[1], geopolygon_gdf.total_bounds[3])
lon_range = (geopolygon_gdf.total_bounds[0], geopolygon_gdf.total_bounds[2])

# Time period
time_range = ("2017-01-01", "2021-12-31")

display_map(x=lon_range, y=lat_range)

Make this Notebook Trusted to load map: File -> Trust Notebook

# # Define the area of interest
# lat = 13.83408
# lon = -16.56464
# lat_buffer = 0.2025
# lon_buffer = 0.1025

# # Time period
# time_range = ("2017-01-01", "2021-12-31")

# # Combine central lat,lon with buffer to get area of interest
# lat_range = (lat - lat_buffer, lat + lat_buffer)
# lon_range = (lon - lon_buffer, lon + lon_buffer)

# display_map(x=lon_range, y=lat_range)

Load satellite data

The first step in the analysis is to load Landsat 8 and 9 data for the specified area of interest. This uses the pre-defined load_ard utility function. The load_ard function is used here to load an analysis ready dataset free of shadow, and missing data.

Note that specifying the parameter min_gooddata=0.9 reduces data from the middle of the year, when this area experiences maximum cloudy weather.

query = {
    "x": lon_range,
    "y": lat_range,
    "time": time_range,
    "resolution": (-30, 30),
    "align": (15, 15),
}

output_crs = mostcommon_crs(dc=dc, product='ls8_sr', query=query)

ds = load_ard(
    dc=dc,
    products=['ls8_sr', 'ls9_sr'],
    measurements=["red", "green", "blue", "nir"],
    group_by="solar_day",
    dask_chunks={"time": 1, "x": 2000, "y": 2000},
    output_crs=output_crs,
    min_gooddata=0.9,
    **query
)

/opt/venv/lib/python3.10/site-packages/deafrica_tools/datahandling.py:244: UserWarning: Setting 'min_gooddata' percentage to > 0.0 will cause dask arrays to compute when loading pixel-quality data to calculate 'good pixel' percentage. This can slow the return of your dataset.
  warnings.warn(

Using pixel quality parameters for USGS Collection 2
Finding datasets
    ls8_sr
    ls9_sr
Counting good quality pixels for each time step
Filtering to 39 out of 114 time steps with at least 90.0% good quality pixels
Applying pixel quality/cloud mask
Re-scaling Landsat C2 data
Returning 39 time steps as a dask array

Load WOfS

Values of NDTI are relative and the index should only be applied to water. Including land in the area of interest will skew the colourmap. All-time WOfS is used here to threshold for areas pixels which are likely to be water.

water = dc.load(
            product="wofs_ls_summary_alltime",
            like=ds.geobox,
            dask_chunks={"time": 1, "x": 2000, "y": 2000}
            )
#extract from mask the areas classified as water
water_extent = (water.frequency > 0.3).squeeze()

print(water_extent)

<xarray.DataArray 'frequency' (y: 1499, x: 750)> Size: 1MB
dask.array<getitem, shape=(1499, 750), dtype=bool, chunksize=(1499, 750), chunktype=numpy.ndarray>
Coordinates:
    time         datetime64[ns] 8B 2003-12-31T23:59:59.999999
  * y            (y) float64 12kB 1.552e+06 1.552e+06 ... 1.508e+06 1.507e+06
  * x            (x) float64 6kB 3.196e+05 3.197e+05 ... 3.421e+05 3.421e+05
    spatial_ref  int32 4B 32628

Inspect water extent

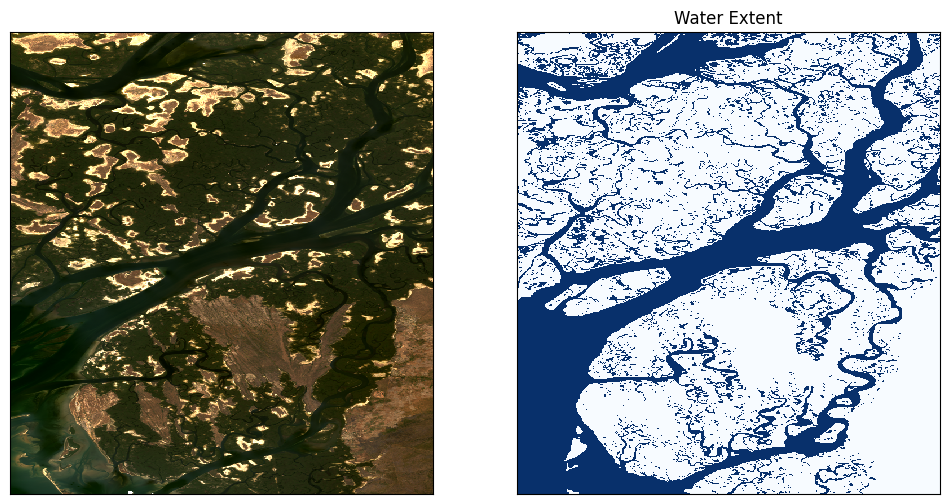
# Plot the geomedian composite and water extent
fig, ax = plt.subplots(1, 2, figsize=(12, 6))

#plot the true colour image
rgb(ds.isel(time=5), ax=ax[0])

#plot the water extent from WOfS
water_extent.plot.imshow(ax=ax[1], cmap="Blues", add_colorbar=False)

# Titles
ax[0].set_title(""), ax[0].xaxis.set_visible(False), ax[0].yaxis.set_visible(False)
ax[1].set_title("Water Extent"), ax[1].xaxis.set_visible(False), ax[1].yaxis.set_visible(False);

Plot NDTI

Here we calculate NDTI and add it to the loaded data set. It also generates an animation that is exported to the sandbox and can be saved by right-clicking the .gif and selecting “Download”.

ds = calculate_indices(ds.where(water_extent), index="NDTI", satellite_mission="ls")

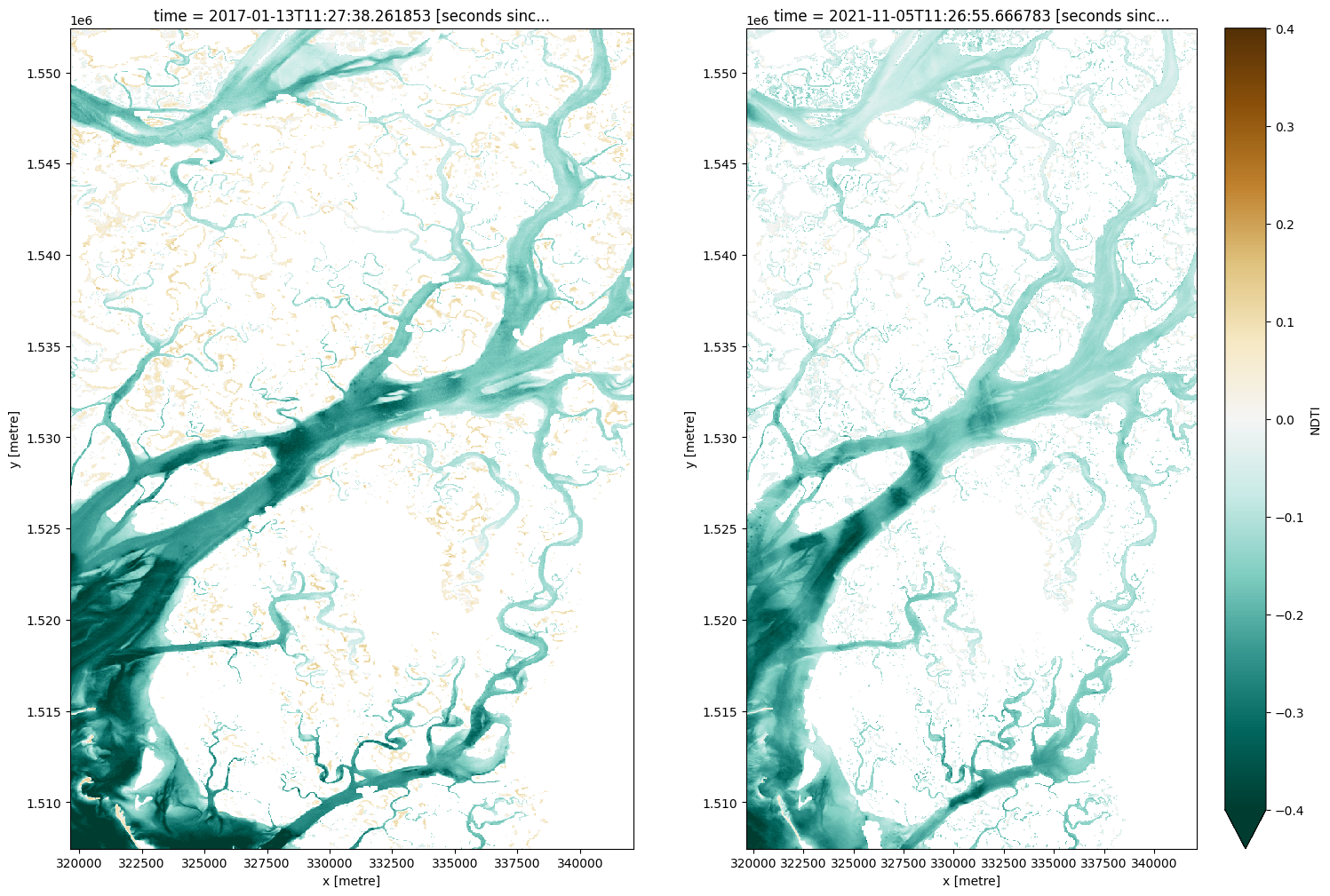
fig, ax = plt.subplots(1, 2, figsize=(18, 12))
cmap='BrBG_r'
vmin=-0.4
vmax=0.4

ds.NDTI.isel(time=0).plot(ax=ax[0], cmap=cmap, add_colorbar=False, vmin=vmin, vmax=vmax)
ds.NDTI.isel(time=-1).plot(ax=ax[1], cmap=cmap, add_colorbar=True, vmin=vmin, vmax=vmax);

# Produce time series animation of NDTI
xr_animation(ds=ds,
             output_path='NDTI_'+time_range[0]+'_'+time_range[1]+'.gif',
             bands=['NDTI'],
             show_text='NDTI',
             interval=250,
             imshow_kwargs={'cmap': 'BrBG_r', 'vmin': vmin, 'vmax': vmax},
             width_pixels=300)

# Plot animated gif
plt.close()
Image(filename='NDTI_'+time_range[0]+'_'+time_range[1]+'.gif')

Exporting animation to NDTI_2017-01-01_2021-12-31.gif

<IPython.core.display.Image object>

Investigate size of waterbodies

The animated timeseries and plots above show a distinct difference in NDTI between large watercourses which generally appear blue-white, and smaller waterbodies which appear more orange to brown in the colour scheme.

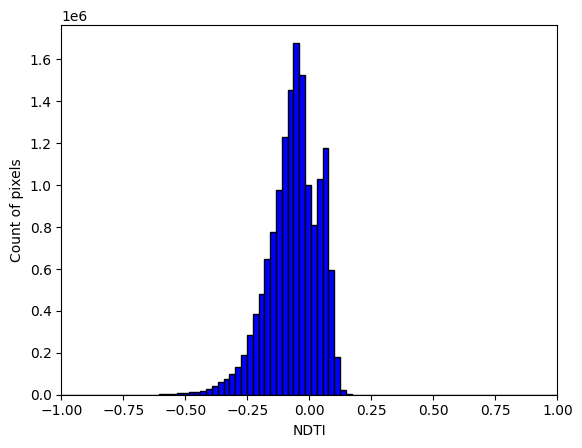
We might hypothesise that smaller waterbodies generally have higher NDTI values than larger ones, meaning they are more turbid. The histogram below suggests this might be the case as there are two peaks evident. We can test this further by splitting the the waterbodies by size below.

plt.hist(ds.NDTI.to_numpy().flatten(), color = 'blue', edgecolor = 'black',
         bins = 8000)
plt.xlim((-1,1))

# Add labels
plt.xlabel('NDTI')
plt.ylabel('Count of pixels')

Text(0, 0.5, 'Count of pixels')

Vectorize waterbodies

We will split the waterbodies into two size classes, small and large, at a threshold of 50,000 square metres. You can adjust the threshold and test it in the plots below.

polygons = xr_vectorize(water_extent, crs='epsg:32628', mask=water_extent==True)
polygons['area'] = polygons.area
polygons['size'] = np.where(polygons['area']<50000, 1, 2) # se

The interactive plot below shows larger waterbodies in yellow and smaller ones in purple.

map_shapefile(polygons, attribute='size')

Here, we rasterize polygons and mask NDTI to small and large waterbodies, then calculate mean and standard deviation timeseries. This allows us to plot the timeseries in the cell below. The plot confirms that smaller waterbodies have higher NDTI values than larger ones, and the two size classes follow the same pattern over time.

water_size = xr_rasterize(gdf=polygons, da=water, attribute_col='size')

ds_large = ds.where(water_size==2)
ds_small = ds.where(water_size==1)

NDTI_ts_large = ds_large.NDTI.mean(['x','y'])
NDTI_ts_small = ds_small.NDTI.mean(['x','y'])
NDTI_ts_large_std = ds_large.NDTI.std(['x','y'])
NDTI_ts_small_std = ds_small.NDTI.std(['x','y'])

fig, ax = plt.subplots(1, 1, figsize=(11, 5))
NDTI_ts_large.plot(ax=ax, label='Large waterbodies', linestyle='dashed', marker='o')
NDTI_ts_small.plot(ax=ax, label='Small waterbodies', linestyle='dashed', marker='o')
ax.fill_between(
    NDTI_ts_large.time,
    NDTI_ts_large-NDTI_ts_large_std,
    NDTI_ts_large+NDTI_ts_large_std,
    alpha=0.2,
)
ax.fill_between(
    NDTI_ts_small.time,
    NDTI_ts_small-NDTI_ts_small_std,
    NDTI_ts_small+NDTI_ts_small_std,
    alpha=0.2,
)
plt.legend(loc="upper left")
plt.title("")
plt.xlabel("");

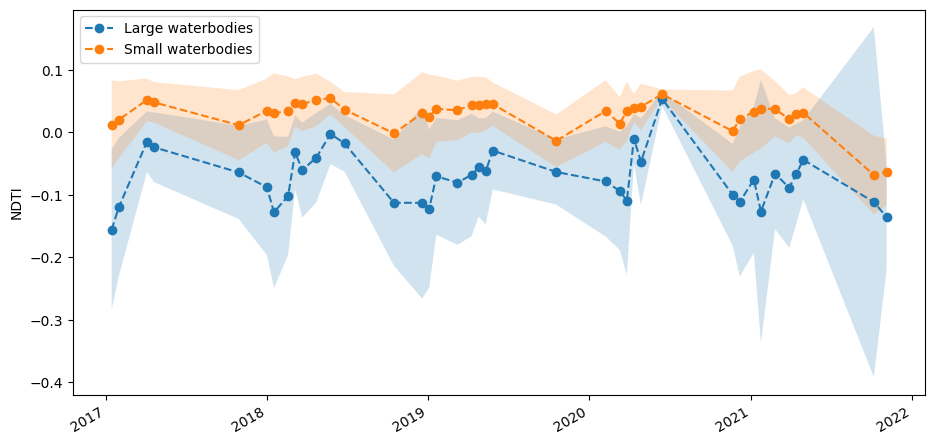
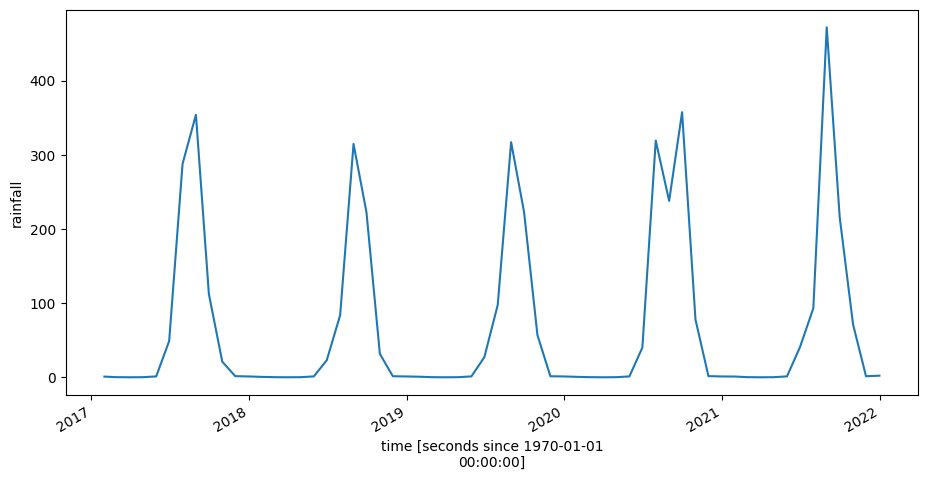
Finally, we might hypothesise that the seasonal variation in turbidity seen above is related to rainfall. The plot of rainfall over the same time period, below, suggests this is the case. However, we would have to conduct further analysis to determine conditions that vary with turbidity.

ds_rf_month = dc.load(product='rainfall_chirps_monthly',
                resolution=(-5000, 5000),
                output_crs='epsg:6933',
                x = lon_range,
                y = lat_range,
                time = time_range)

ds_rf_month.resample(time='1M').mean().rainfall.mean(['x','y']).plot(figsize=(11, 5))
plt.title("");

<string>:6: FutureWarning: 'M' is deprecated and will be removed in a future version. Please use 'ME' instead of 'M'.

---

Additional information

License The code in this notebook is licensed under the Apache License, Version 2.0.

Digital Earth Africa data is licensed under the Creative Commons by Attribution 4.0 license.

Contact If you need assistance, please post a question on the DE Africa Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here).

If you would like to report an issue with this notebook, you can file one on Github.

Compatible datacube version

print(datacube.__version__)

1.8.19

Last Tested:

from datetime import datetime
datetime.today().strftime('%Y-%m-%d')

'2024-11-05'