Digital Elevation Models¶
Products used: dem_cop_30, dem_cop_90, dem_srtm, dem_srtm_deriv
Keywords: :index: “data used; Copernicus DEM 30 m”, :index: “data used; Copernicus DEM 90 m”, :index: “data used; 1 second elevation model”, :index: “data used; 1 second elevation model derivatives”, data used; ERA5, :index: “datasets; dem_cop_30”, :index: “datasets; dem_cop_90”, :index: “datasets; dem_srtm”, :index: “datasets; dem_srtm_deriv”
Contexte¶
Digital Elevation Models (DEMs) provide information on bare ground topography, that is, elevation irrespective of land cover such as buildings/trees. DEMs are often derived from Light Detection and Ranging (LiDAR) data sources. DEMs are used in several applications such as understanding how climatic variables change with topography.
Important details:
There are four DEM products available from the Open Data Cube. The Copernicus products come from the European Space Agency (ESA) and the Shuttle Radar Topography Mission (SRTM) products are from the United States Geological Survey (USGS):
Copernicus DEM 30 m:
dem_cop_30, elevation data at 30 m resolutionCopernicus DEM 90 m:
dem_cop_90, elevation data at 90 m resolutionDEM SRTM:
dem_srtm, elevation data at 1-arc second (~30 m)DEM SRTM Derivatives:
dem_srtm_deriv, derivatives of the 1-arc second DEM which include:Slope (percent); this is the rate of elevation change, so mathematically speaking it is the first/primary derivative of elevation.
Multi-resolution Valley Bottom Flatness (MrVBF); this identifies valley bottoms (areas of deposition). Zero values indicate erosional terrain and values ≥1 and indicate progressively larger areas of deposition.
Multi-resolution Ridge Top Flatness (MrRTF); complementary to MrVBF, zero values indicate areas that are steep or low, and values ≥1 indicate progressively larger areas of high flat land.
For further details on how these measurements were calculated see the DEM derivatives repository
Description¶
In this notebook we will load the Copernicus 30 m DEM and the DEM derivatives using dc.load(). Then we run through a short example analysis.
Topics covered include: 1. Inspecting the DEM product available in the datacube 2. Using the dc.load() function to load in DEM data 3. Plotting DEM and derivatives 4. An example analysis which compares temperature at high and low elevation
Getting started¶
To run this analysis, run all the cells in the notebook, starting with the « Load packages » cell.
Load packages¶
[1]:
%matplotlib inline
import datacube
import numpy as np
import xarray as xr
import matplotlib.pyplot as plt
from deafrica_tools.plotting import display_map
from deafrica_tools.load_era5 import load_era5
from odc.algo import xr_reproject
Connect to the datacube¶
[2]:
dc = datacube.Datacube(app="DEM")
List measurements¶
The table below lists the products and measurements available for the DEM datasets indexed within DE Africa’s datacube. We can see that the first three products contain a single measure for elevation, expressed in metres above sea level. The derivatives product comprises percent slope, multi-resolution valley bottom flatness (mrvbf), and multi-resolution ridge top flatness (mrrtf).
[3]:
product_name = ['dem_cop_30', 'dem_cop_90', 'dem_srtm', 'dem_srtm_deriv']
dc_measurements = dc.list_measurements()
dc_measurements.loc[product_name].drop('flags_definition', axis=1)
[3]:
| name | dtype | units | nodata | aliases | ||
|---|---|---|---|---|---|---|
| product | measurement | |||||
| dem_cop_30 | elevation | elevation | float32 | 1 | NaN | NaN |
| dem_cop_90 | elevation | elevation | float32 | 1 | NaN | NaN |
| dem_srtm | elevation | elevation | int16 | metre | -32768.0 | NaN |
| dem_srtm_deriv | mrvbf | mrvbf | int16 | 1 | -32768.0 | NaN |
| mrrtf | mrrtf | int16 | 1 | -32768.0 | NaN | |
| slope | slope | float32 | 1 | -9999.0 | NaN |
Analysis parameters¶
lat,lon: The central latitude and longitude to analyse (e.g. -3.0674, 37.355).buffer: The number of square degrees to load around the central latitude and longitude. For reasonable loading times, set this as 0.1 or lower.resolution: We use 30 m here for thedem_cop_30product.
[4]:
lat, lon = -3.0674, 37.3556 #Mt Kilimanjaro
buffer = 0.3
resolution=(-30, 30)
measurements='elevation'
#convert the lat,lon,buffer into a range
lons = (lon - buffer, lon + buffer)
lats = (lat - buffer, lat + buffer)
View the selected location¶
The next cell will display the selected area on an interactive map. Feel free to zoom in and out to get a better understanding of the area you’ll be analysing. Clicking on any point of the map will reveal the latitude and longitude coordinates of that point.
[5]:
display_map(x=lons, y=lats)
[5]:
Load the Copernicus 30 m DEM data¶
[6]:
#set up daatcube query object
query = {
'x': lons,
'y': lats,
'resolution':resolution,
'output_crs': 'epsg:6933',
'measurements':measurements
}
#load the dem 30 m product
ds = dc.load(product="dem_cop_30", **query).squeeze()
print(ds)
<xarray.Dataset>
Dimensions: (y: 2549, x: 1931)
Coordinates:
time datetime64[ns] 2000-01-01T12:00:00
* y (y) float64 -3.529e+05 -3.529e+05 ... -4.293e+05 -4.293e+05
* x (x) float64 3.575e+06 3.575e+06 ... 3.633e+06 3.633e+06
spatial_ref int32 6933
Data variables:
elevation (y, x) float32 1.147e+03 1.146e+03 1.148e+03 ... 851.2 854.4
Attributes:
crs: epsg:6933
grid_mapping: spatial_ref
Plot elevation¶
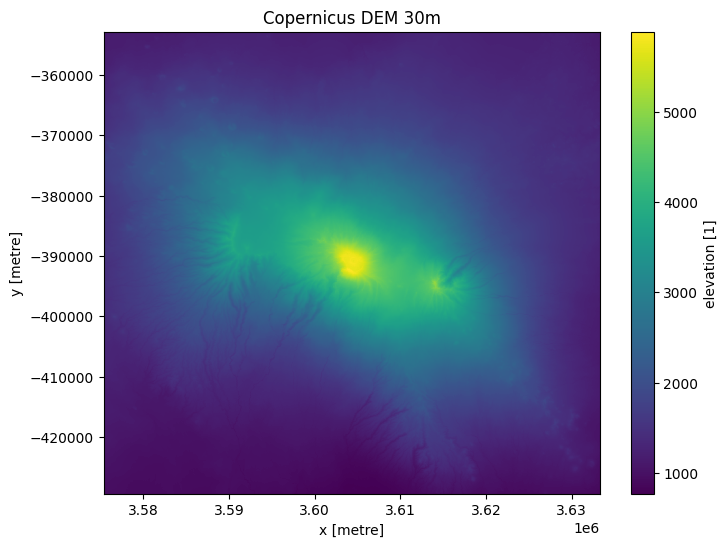
We can generate a basic plot of elevation below. The summit of Mt Kilimanjaro is 5,895m.
[7]:
ds.elevation.plot(figsize=(8,6))
plt.title('Copernicus DEM 30m');
Load DEM deriviatives¶
Now we can load the derivative dataset with the same parameters, except measurements.
[8]:
# We just need to change the measurements parameter, lats, lon, crs etc. can remain the same.
measurements=['mrvbf', 'mrrtf', 'slope']
query = {
'x': lons,
'y': lats,
'resolution':resolution,
'output_crs': 'epsg:6933',
'measurements':measurements
}
ds_deriv = dc.load(product="dem_srtm_deriv", **query).squeeze()
print(ds_deriv)
<xarray.Dataset>
Dimensions: (y: 2549, x: 1931)
Coordinates:
time datetime64[ns] 2000-01-01T12:00:00
* y (y) float64 -3.529e+05 -3.529e+05 ... -4.293e+05 -4.293e+05
* x (x) float64 3.575e+06 3.575e+06 ... 3.633e+06 3.633e+06
spatial_ref int32 6933
Data variables:
mrvbf (y, x) int16 2 1 0 0 3 4 4 3 3 3 3 3 ... 0 1 0 0 0 1 2 2 2 1 1
mrrtf (y, x) int16 0 0 1 1 0 0 0 0 0 0 1 0 ... 2 2 1 0 0 0 0 0 0 0 0
slope (y, x) float32 7.383 12.15 13.24 10.62 ... 2.5 4.29 8.271 9.148
Attributes:
crs: epsg:6933
grid_mapping: spatial_ref
Plot derivatives¶
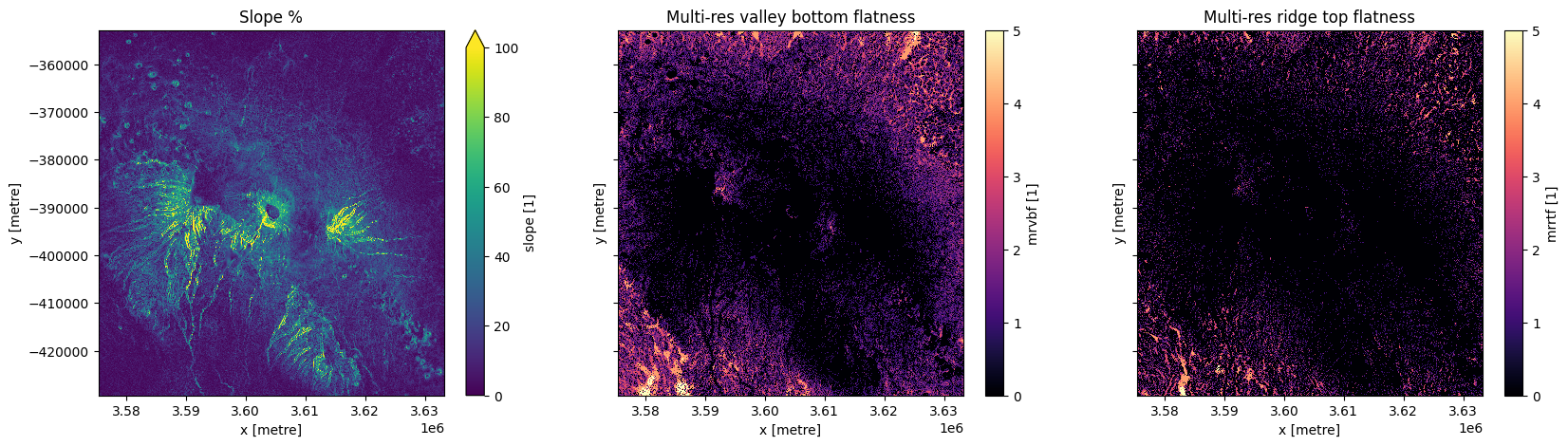
Plotting the three derivative measurements below shows areas of greater steepness around Mt Kilimanjaro. Most of the mountain has a 0 value for valley bottom and ridge tip flatness, whereas surrounding areas are identified as valleys and flat ridge tops.
[9]:
fig,ax = plt.subplots(1,3, figsize=(20,5), sharey=True)
ds_deriv.slope.plot(ax=ax[0], vmax=100)
ds_deriv.mrvbf.plot(ax=ax[1], cmap='magma')
ds_deriv.mrrtf.plot(ax=ax[2], cmap='magma')
ax[0].set_title('Slope %')
ax[1].set_title('Multi-res valley bottom flatness')
ax[2].set_title('Multi-res ridge top flatness');
Analysis example: masking based on elevation¶
We can use elevation information to select or mask areas for analysis. In this example, we will compare climatic information between higher and lower elevation at the Virunga Mountains, a chain of volcanoes along the border of Rwanda, the Democratic Republic of the Congo, and Uganda.
Below we set up some new analysis parameters:
lat,lon: The central latitude and longitude to analyse for the Virunga Mountains (-1.4310, 29.5262).buffer: The number of square degrees to load around the central latitude and longitude.resolution: We use 90 m here with thedem_cop_90product for faster loading and computation times.
[10]:
lat, lon = -1.4310, 29.5262
buffer = 0.2
resolution=(-90, 90)
measurements='elevation'
#convert the lat,lon,buffer into a range
lons = (lon - buffer, lon + buffer)
lats = (lat - buffer, lat + buffer)
View the selected location¶
[11]:
display_map(x=lons, y=lats)
[11]:
Load the Copernicus 90m DEM¶
[12]:
query = {
'x': lons,
'y': lats,
'resolution':resolution,
'output_crs': 'epsg:6933',
'measurements':measurements
}
#load the dem
ds = dc.load(product="dem_cop_90", **query).squeeze() # Using 90 m product for better computation times
[13]:
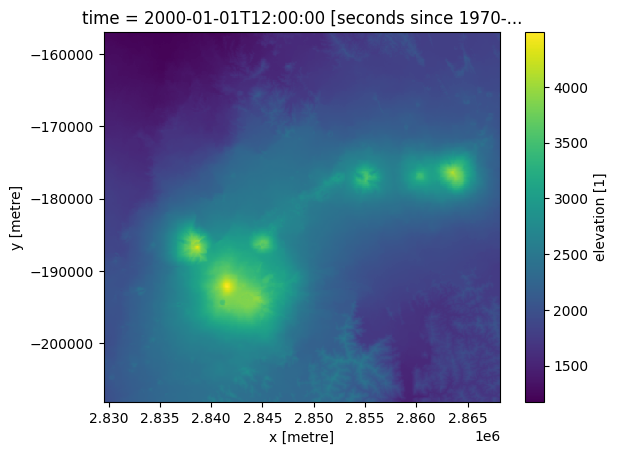
ds.elevation.plot();
Mask analysis to high and low elevation¶
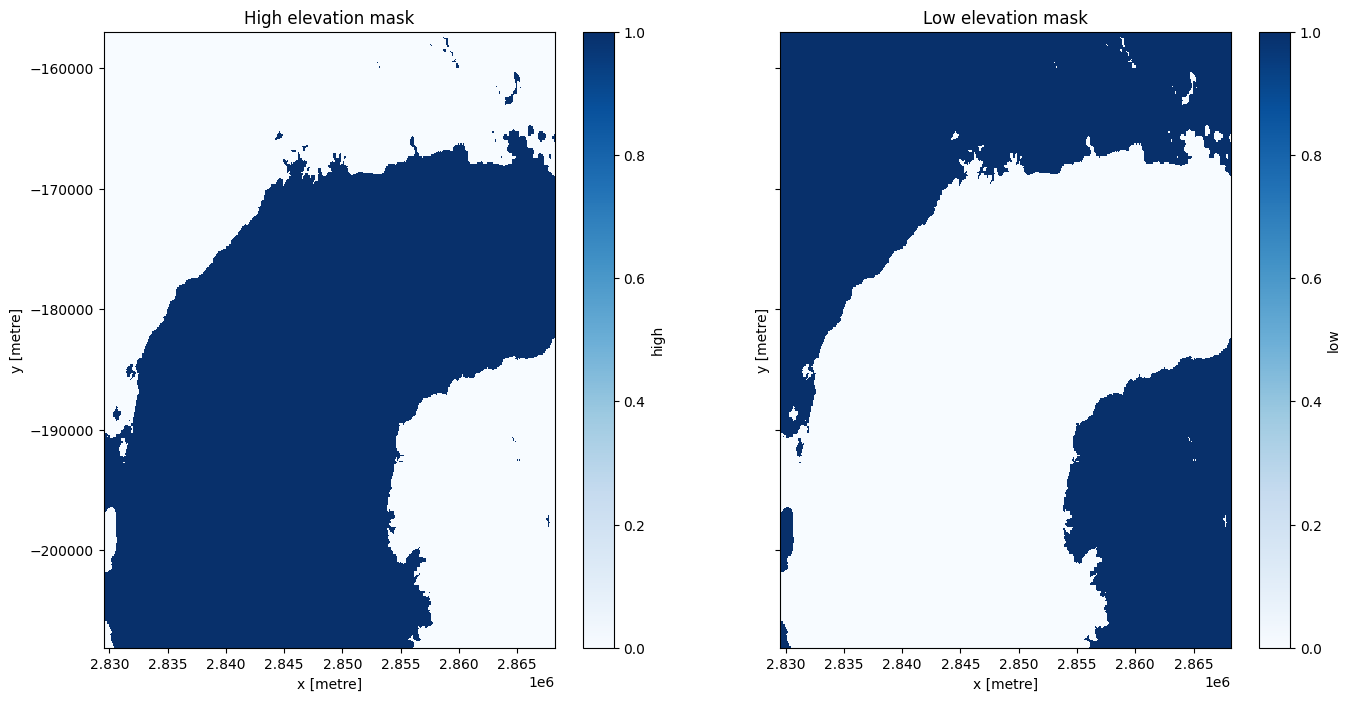
For this analysis, we will split the dataset into areas above and below 2,000m in elevation. In the plot below we can see that this separates the chain of volcanoes from surrounding lowland.
[14]:
ds = ds.assign(high=xr.where(ds.elevation >= 2000, 1, 0))
ds = ds.assign(low=xr.where(ds.elevation < 2000, 1, 0))
print(ds)
<xarray.Dataset>
Dimensions: (y: 568, x: 430)
Coordinates:
time datetime64[ns] 2000-01-01T12:00:00
* y (y) float64 -1.57e+05 -1.571e+05 ... -2.079e+05 -2.08e+05
* x (x) float64 2.83e+06 2.83e+06 2.83e+06 ... 2.868e+06 2.868e+06
spatial_ref int32 6933
Data variables:
elevation (y, x) float32 1.237e+03 1.235e+03 ... 1.765e+03 1.793e+03
high (y, x) int64 0 0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0 0
low (y, x) int64 1 1 1 1 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1 1 1 1 1
Attributes:
crs: epsg:6933
grid_mapping: spatial_ref
[15]:
fig, axes = plt.subplots(1, 2, figsize=(16, 8), sharey=True)
ds.high.plot(cmap='Blues', ax=axes[0])
ds.low.plot(cmap='Blues', ax=axes[1])
axes[0].set_title('High elevation mask')
axes[1].set_title('Low elevation mask');
Load temperature data and compare between high and low elevation¶
We will use the load_era5 function to load temperature data. More information on loading and using climate data can be found in the Climate_Data_ERA5_AWS Datasets notebook.
[16]:
time = time = '2021-01', '2021-03' # first three months of 2021
temp_var = 'air_temperature_at_2_metres'
temp_mean = load_era5(temp_var, lats, lons, time, reduce_func=np.mean, resample='1D').compute()-273.15 # Convert Kelvin to Celsius
To make our calculation we will need to reproject the climate data so it matches the elevation data. We use the xr_reproject function to do this. More information on reprojecting datacube data is available here.
[17]:
temp_mean_reprojected = xr_reproject(temp_mean, ds.geobox, resampling="average")
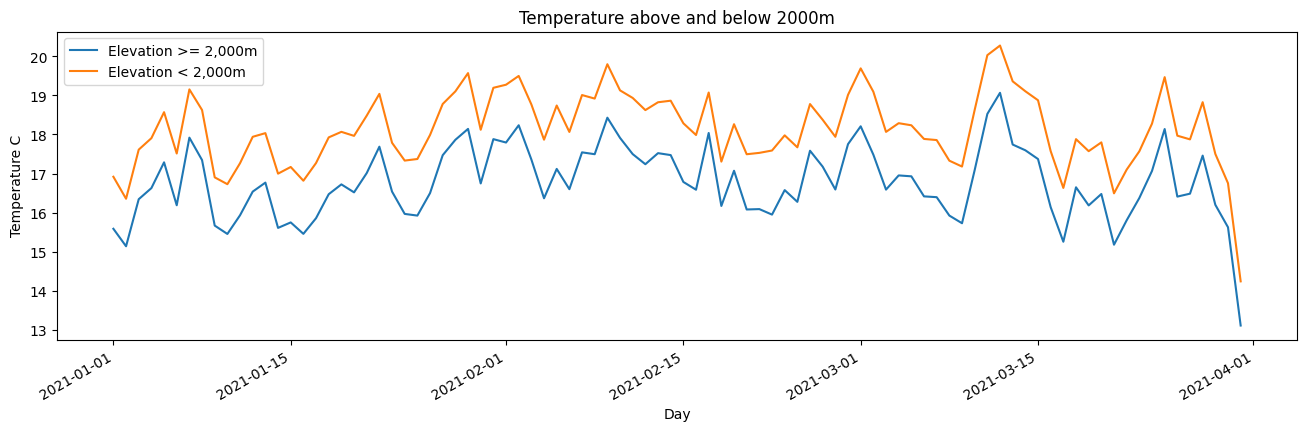
We can see that average daily temperature tends to be lower at the altitudes >2,000m for our analysis area, according to the ERA5 reanalysis product.
[18]:
ds = ds.merge(temp_mean_reprojected, ds)
ds_high = ds.where(ds.squeeze().high)
high_mean_airtemp = ds_high.air_temperature_at_2_metres.mean(['x','y'])
ds_low = ds.where(ds.squeeze().low)
low_mean_airtemp = ds_low.air_temperature_at_2_metres.mean(['x','y'])
ds_high.air_temperature_at_2_metres.mean(['x','y']).plot(figsize = (16,4), label='Elevation >= 2,000m');
ds_low.air_temperature_at_2_metres.mean(['x','y']).plot(label='Elevation < 2,000m');
plt.legend();
plt.xlabel('Day');
plt.ylabel('Temperature C')
plt.title('Temperature above and below 2000m');
Additional information¶
License: The code in this notebook is licensed under the Apache License, Version 2.0. Digital Earth Africa data is licensed under the Creative Commons by Attribution 4.0 license.
Contact: If you need assistance, please post a question on the Open Data Cube Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here). If you would like to report an issue with this notebook, you can file one on
Github.
Compatible datacube version:
[19]:
print(datacube.__version__)
1.8.15
Last tested:
[20]:
from datetime import datetime
datetime.today().strftime('%Y-%m-%d')
[20]:
'2023-08-11'