Radar vegetation phenology using Sentinel-1¶
Keywords data used; sentinel-1, data used; crop_mask, band index; RVI, phenology, analysis; time series
Contexte¶
Phenology is the study of plant and animal life cycles in the context of the seasons. It can be useful in understanding the life cycle trends of crops and how the growing seasons are affected by changes in climate. However, in cloudy regions optical satellites may not view the vegetation cycle during key moments of growth (e.g. during the peak of the growing sesaon) leading to inaccurate estimates of vegetation phenology variables. The Sentinel-1 radar satellite “sees” through clouds and can, in theory, view the entire life cycle of plants. This notebook will use Sentinel-1 to derive key phenology statistics. You can compare these results with the results from the Sentinel-2 vegetation phenology notebook which relies on optical data to calculate phenology over the same region as this notebook
Description¶
This notebook demonstrates how to calculate vegetation phenology statistics over cropping regions using the DE Africa function xr_phenology. To detect changes in plant life for Sentinel-1, the script uses the Radar Vegetation Index
The outputs of this notebook can be used to assess spatio-temporal differences in the growing seasons of agriculture fields or native vegetation.
This notebook demonstrates the following steps:
Load Sentinel 1 data for an area of interest.
Mask region with DE Africa’s cropland extent map
Calculate the radar vegetation index.
Plot false colour images of the region.
Compute the radar vegetation index
Smooth the vegetation timeseries to minimize noise.
Calculate phenology statistics on a simple 1D vegetation time series
Calculate per-pixel phenology statistics
Getting started¶
To run this analysis, run all the cells in the notebook, starting with the « Load packages » cell.
Load packages¶
Load key Python packages and supporting functions for the analysis.
[1]:
%matplotlib inline
# Force GeoPandas to use Shapely instead of PyGEOS
# In a future release, GeoPandas will switch to using Shapely by default.
import os
os.environ['USE_PYGEOS'] = '0'
import datetime as dt
import os
import datacube
import matplotlib.pyplot as plt
import numpy as np
import geopandas as gpd
from datacube.utils.aws import configure_s3_access
from deafrica_tools.bandindices import dualpol_indices
from deafrica_tools.classification import HiddenPrints
from deafrica_tools.datahandling import load_ard
from deafrica_tools.plotting import display_map, rgb
from deafrica_tools.temporal import xr_phenology
from datacube.utils.geometry import Geometry
from deafrica_tools.spatial import xr_rasterize
from deafrica_tools.areaofinterest import define_area
configure_s3_access(aws_unsigned=True, cloud_defaults=True)
Connect to the datacube¶
Connect to the datacube so we can access DE Africa data. The app parameter is a unique name for the analysis which is based on the notebook file name.
[2]:
dc = datacube.Datacube(app="Radar_vegetation_phenology")
Analysis parameters¶
The following cell sets important parameters for the analysis:
lat: The central latitude to analyse (e.g.-10.6996).lon: The central longitude to analyse (e.g.35.2708).buffer: The number of square degrees to load around the central latitude and longitude. For reasonable loading times, set this as0.1or lower.time_range: The year range to analyse (e.g.('2019-01', '2020-12')).
Select location¶
To define the area of interest, there are two methods available:
By specifying the latitude, longitude, and buffer. This method requires you to input the central latitude, central longitude, and the buffer value in square degrees around the center point you want to analyze. For example,
lat = 10.338,lon = -1.055, andbuffer = 0.1will select an area with a radius of 0.1 square degrees around the point with coordinates (10.338, -1.055).By uploading a polygon as a
GeoJSON or Esri Shapefile. If you choose this option, you will need to upload the geojson or ESRI shapefile into the Sandbox using Upload Files button in the top left corner of the Jupyter Notebook interface. ESRI shapefiles must be uploaded with all the related files
in the top left corner of the Jupyter Notebook interface. ESRI shapefiles must be uploaded with all the related files (.cpg, .dbf, .shp, .shx). Once uploaded, you can use the shapefile or geojson to define the area of interest. Remember to update the code to call the file you have uploaded.
To use one of these methods, you can uncomment the relevant line of code and comment out the other one. To comment out a line, add the "#" symbol before the code you want to comment out. By default, the first option which defines the location using latitude, longitude, and buffer is being used.
[3]:
# Method 1: Specify the latitude, longitude, and buffer
aoi = define_area(lat=8.7186, lon=40.8646, buffer=0.02)
# Method 2: Use a polygon as a GeoJSON or Esri Shapefile.
# aoi = define_area(vector_path='aoi.shp')
#Create a geopolygon and geodataframe of the area of interest
geopolygon = Geometry(aoi["features"][0]["geometry"], crs="epsg:4326")
geopolygon_gdf = gpd.GeoDataFrame(geometry=[geopolygon], crs=geopolygon.crs)
# Get the latitude and longitude range of the geopolygon
lat_range = (geopolygon_gdf.total_bounds[1], geopolygon_gdf.total_bounds[3])
lon_range = (geopolygon_gdf.total_bounds[0], geopolygon_gdf.total_bounds[2])
# Set the range of dates for the analysis
time_range = ("2019-01-01", "2020-12-20")
View the selected location¶
The next cell will display the selected area on an interactive map. Feel free to zoom in and out to get a better understanding of the area you’ll be analysing. Clicking on any point of the map will reveal the latitude and longitude coordinates of that point.
[4]:
display_map(x=lon_range, y=lat_range)
[4]:
Load Sentinel-1 data¶
The first step is to load Sentinel-1 data for the specified area of interest and time range. The load_ard function is used here to load data that has been masked using quality filters, making it ready for analysis.
[5]:
# Create a reusable query
query = {
"y": lat_range,
"x": lon_range,
"time": time_range,
"measurements": ["vv", "vh"],
"resolution": (-20, 20),
"output_crs": "epsg:6933",
"group_by": "solar_day",
}
# Load available data from Sentinel-1
ds = load_ard(
dc=dc,
products=["s1_rtc"],
**query,
)
print(ds)
Using pixel quality parameters for Sentinel 1
Finding datasets
s1_rtc
Applying pixel quality/cloud mask
Loading 111 time steps
/usr/local/lib/python3.10/dist-packages/rasterio/warp.py:344: NotGeoreferencedWarning: Dataset has no geotransform, gcps, or rpcs. The identity matrix will be returned.
_reproject(
<xarray.Dataset>
Dimensions: (time: 111, y: 253, x: 194)
Coordinates:
* time (time) datetime64[ns] 2019-01-01T03:01:22.069586 ... 2020-12...
* y (y) float64 1.111e+06 1.111e+06 ... 1.106e+06 1.106e+06
* x (x) float64 3.941e+06 3.941e+06 ... 3.945e+06 3.945e+06
spatial_ref int32 6933
Data variables:
vv (time, y, x) float32 0.105 0.1644 0.1272 ... 0.2308 0.1722
vh (time, y, x) float32 0.02471 0.02468 ... 0.03206 0.02134
Attributes:
crs: epsg:6933
grid_mapping: spatial_ref
Clip the datasets to the shape of the area of interest¶
A geopolygon represents the bounds and not the actual shape because it is designed to represent the extent of the geographic feature being mapped, rather than the exact shape. In other words, the geopolygon is used to define the outer boundary of the area of interest, rather than the internal features and characteristics.
Clipping the data to the exact shape of the area of interest is important because it helps ensure that the data being used is relevant to the specific study area of interest. While a geopolygon provides information about the boundary of the geographic feature being represented, it does not necessarily reflect the exact shape or extent of the area of interest.
[6]:
#Rasterise the area of interest polygon
aoi_raster = xr_rasterize(gdf=geopolygon_gdf, da=ds, crs=ds.crs)
#Mask the dataset to the rasterised area of interest
ds = ds.where(aoi_raster == 1)
Mask region with DE Africa’s cropland extent map¶
Load the cropland mask over the region of interest.
[7]:
cm = dc.load(
product="crop_mask",
time=("2019"),
measurements="filtered",
resampling="nearest",
like=ds.geobox,
).filtered.squeeze()
cm.where(cm < 255).plot.imshow(
add_colorbar=False, figsize=(6, 6)
) # we filter to <255 to omit missing data
plt.title("Cropland Extent");
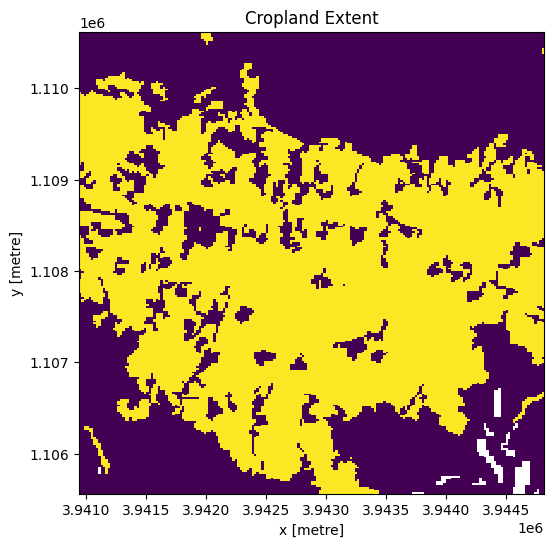
Now we will use the cropland map to mask the regions in the Sentinel-1 data that only have cropping.
[8]:
# Filter out the no-data pixels (255) and non-crop pixels (0) from the cropland map and
# mask the Sentinel-1 data.
ds = ds.where(cm == 1)
False colour RGB plots¶
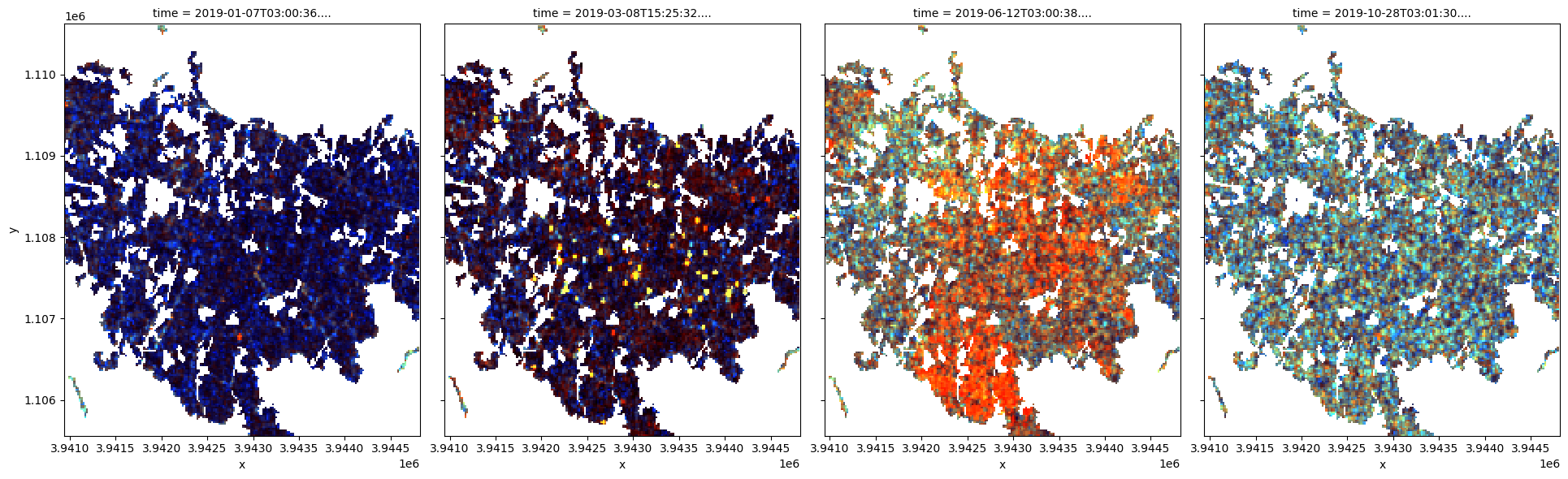
Now can plot some of the Sentinel-1 images as false colour images using the rgb function. Notice that the backscatter intensity of the cropping regions is changing throughout the year as the plants in the fields go through their growth and senescence cycle.
[9]:
# VH/VV will help create an RGB image
ds["vh/vv"] = ds.vh / ds.vv
# median values are used to scale the measurements so they have a similar range for visualization
med_s1 = ds[["vv", "vh", "vh/vv"]].median()
[10]:
# plotting an RGB image for selected timesteps
time_steps = [1, 10, 22, 45]
rgb(
ds[["vv", "vh", "vh/vv"]] / med_s1, # normalize image ranges
bands=["vv", "vh", "vh/vv"],
index=time_steps,
col_wrap=4,
);
Compute the radar vegetation index¶
This study measures the presence of vegetation through either the Radar vegetation index (RVI).
The formula is
RVI = 4*VH/(VV+VH)
RVI is available through the dualpol_indices function, imported from deafrica_tools.bandindices.
[11]:
# Calculate the chosen vegetation proxy index and add it to the loaded data set
ds = dualpol_indices(ds, index="RVI")
Plot the vegetation index over time¶
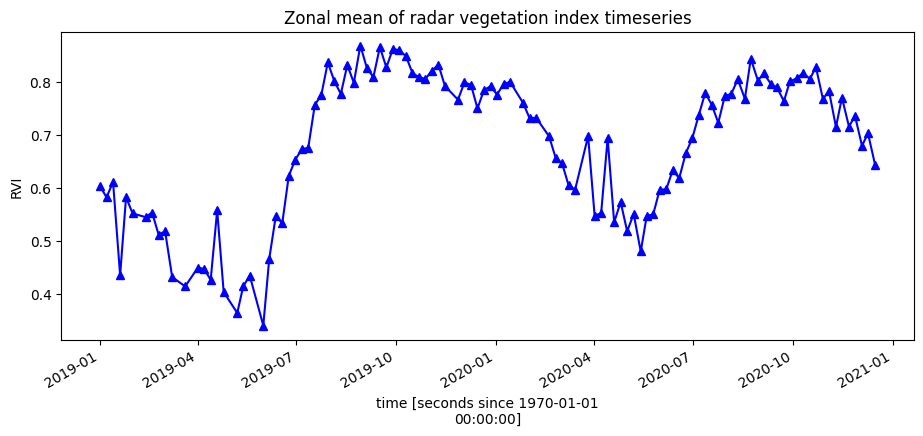
To get an idea of how the vegetation health changes throughout the year(s), we can plot a zonal time series over the region of interest. First we will do a simple plot of the zonal mean of the data.
[12]:
ds.RVI.mean(["x", "y"]).plot.line("b-^", figsize=(11, 4))
plt.title("Zonal mean of radar vegetation index timeseries");
Smoothing/Interpolating vegetation time-series¶
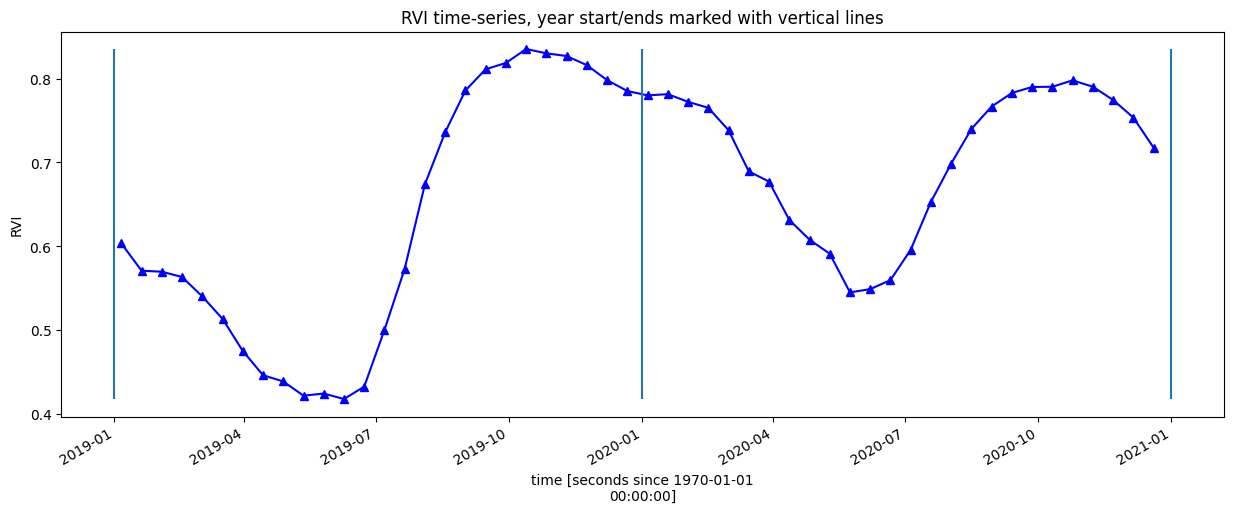
Here, we will smooth and interpolate the data to ensure we working with a consistent time-series. This is a very important step in the workflow and there are many ways to smooth, interpolate, gap-fill, remove outliers, or curve-fit the data to ensure a useable time-series. If not using the default example, you may have to define additional methods to those used here.
To do this we take two steps:
Resample the data to fortnightly time-steps using the fortnightly median
Calculate a rolling mean with a window of 4 steps
[13]:
resample_period = "2W"
window = 4
rvi_smooth = (
ds.RVI.resample(time=resample_period)
.median()
.rolling(time=window, min_periods=1)
.mean()
)
Plot the smoothed and interpolated time-series
[14]:
rvi_smooth_1D = rvi_smooth.mean(["x", "y"])
rvi_smooth_1D.plot.line("b-^", figsize=(15, 5))
_max = rvi_smooth_1D.max()
_min = rvi_smooth_1D.min()
plt.vlines(np.datetime64("2019-01-01"), ymin=_min, ymax=_max)
plt.vlines(np.datetime64("2020-01-01"), ymin=_min, ymax=_max)
plt.vlines(np.datetime64("2021-01-01"), ymin=_min, ymax=_max)
plt.title("RVI time-series, year start/ends marked with vertical lines")
plt.ylabel("RVI");
Calculate phenology statistics using xr_phenology¶
The DE Africa function xr_phenology can calculate a number of land-surface phenology statistics that together describe the characteristics of a plant’s lifecycle. The function can calculate the following statistics on either a zonal timeseries (like the one above), or on a per-pixel basis:
SOS = DOY of start of season
POS = DOY of peak of season
EOS = DOY of end of season
vSOS = Value at start of season
vPOS = Value at peak of season
vEOS = Value at end of season
Trough = Minimum value of season
LOS = Length of season (DOY)
AOS = Amplitude of season (in value units)
ROG = Rate of greening
ROS = Rate of senescence
where DOY = day-of-year (Jan 1st = 0, Dec 31st = 365). By default the function will return all the statistics as an xarray.Dataset, to return only a subset of these statistics pass a list of the desired statistics to the function e.g. stats=['SOS', 'EOS', 'ROG'].
See the deafrica_tools.temporal script for more information on each of the parameters in xr_phenology.
Zonal phenology statistics¶
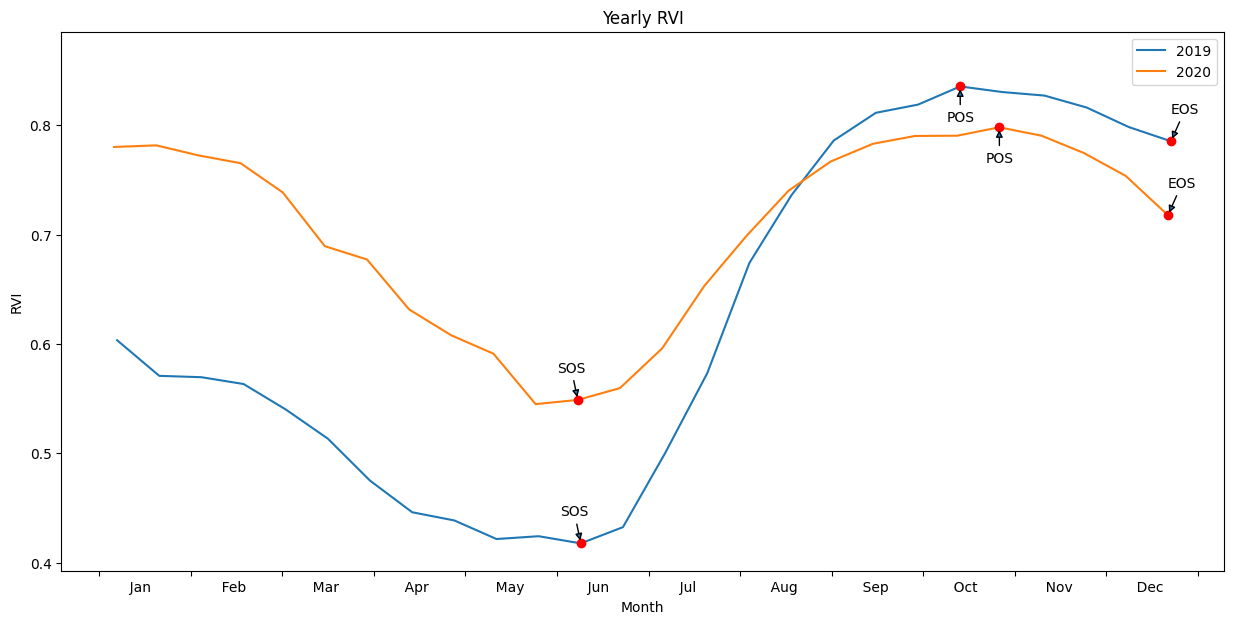
To help us understand what these statistics refer too, lets first pass the simpler zonal mean (mean of all pixels in the image) time-series to the function and plot the results on the same curves as above.
First, provide a list of statistics to calculate with the parameter, pheno_stats.
method_sos : If “first” then vSOS is estimated as the first positive slope on the greening side of the curve. If “median”, then vSOS is estimated as the median value of the postive slopes on the greening side of the curve.
method_eos : If “last” then vEOS is estimated as the last negative slope on the senescing side of the curve. If “median”, then vEOS is estimated as the “median” value of the negative slopes on the senescing side of the curve.
[15]:
pheno_stats = [
"SOS",
"vSOS",
"POS",
"vPOS",
"EOS",
"vEOS",
"Trough",
"LOS",
"AOS",
"ROG",
"ROS",
]
method_sos = "first"
method_eos = "last"
[16]:
# find all the years to assist with plotting
years = rvi_smooth_1D.groupby("time.year")
# get list of years in ts to help with looping
years_int = [y[0] for y in years]
# store results in dict
pheno_results = {}
# loop through years and calculate phenology
for year in years_int:
# select year
da = dict(years)[year]
# calculate stats
stats = xr_phenology(
da,
method_sos=method_sos,
method_eos=method_eos,
stats=pheno_stats,
verbose=False,
)
# add results to dict
pheno_results[str(year)] = stats
for key, value in pheno_results.items():
print("Year: " + key)
for b in value.data_vars:
print(" " + b + ": ", round(float(value[b].values), 3))
Year: 2019
SOS: 160.0
vSOS: 0.418
POS: 286.0
vPOS: 0.835
EOS: 356.0
vEOS: 0.785
Trough: 0.418
LOS: 196.0
AOS: 0.418
ROG: 0.003
ROS: -0.001
Year: 2020
SOS: 159.0
vSOS: 0.549
POS: 299.0
vPOS: 0.798
EOS: 355.0
vEOS: 0.718
Trough: 0.545
LOS: 196.0
AOS: 0.253
ROG: 0.002
ROS: -0.001
Plot the results with our statistcs annotated on the plot
[17]:
# find all the years to assist with plotting
years = rvi_smooth_1D.groupby("time.year")
fig, ax = plt.subplots()
fig.set_size_inches(15, 7)
for year, y in zip(years, years_int):
# grab tall the values we need for plotting
eos = pheno_results[str(y)].EOS.values
sos = pheno_results[str(y)].SOS.values
pos = pheno_results[str(y)].POS.values
veos = pheno_results[str(y)].vEOS.values
vsos = pheno_results[str(y)].vSOS.values
vpos = pheno_results[str(y)].vPOS.values
# create plot
# the groupby and mean below doesn't actually do anything, except allow
# the plots to be on the same x-axis. i.e. veg-data isn't modified, just time units
year[1].groupby("time.dayofyear").mean().plot(ax=ax, label=year[0])
# add start of season
ax.plot(sos, vsos, "or")
ax.annotate(
"SOS",
xy=(sos, vsos),
xytext=(-15, 20),
textcoords="offset points",
arrowprops=dict(arrowstyle="-|>"),
)
# add end of season
ax.plot(eos, veos, "or")
ax.annotate(
"EOS",
xy=(eos, veos),
xytext=(0, 20),
textcoords="offset points",
arrowprops=dict(arrowstyle="-|>"),
)
# add peak of season
ax.plot(pos, vpos, "or")
ax.annotate(
"POS",
xy=(pos, vpos),
xytext=(-10, -25),
textcoords="offset points",
arrowprops=dict(arrowstyle="-|>"),
)
ax.legend()
plt.ylim(_min - 0.025, _max.values + 0.05)
month_abbr = [
"Jan",
"Feb",
"Mar",
"Apr",
"May",
"Jun",
"Jul",
"Aug",
"Sep",
"Oct",
"Nov",
"Dec",
"",
]
new_m = []
for m in month_abbr:
new_m.append(" %s" % m) # Add spaces before the month name
plt.xticks(np.linspace(0, 365, 13), new_m, horizontalalignment="left")
plt.xlabel("Month")
plt.ylabel("RVI")
plt.title("Yearly RVI");
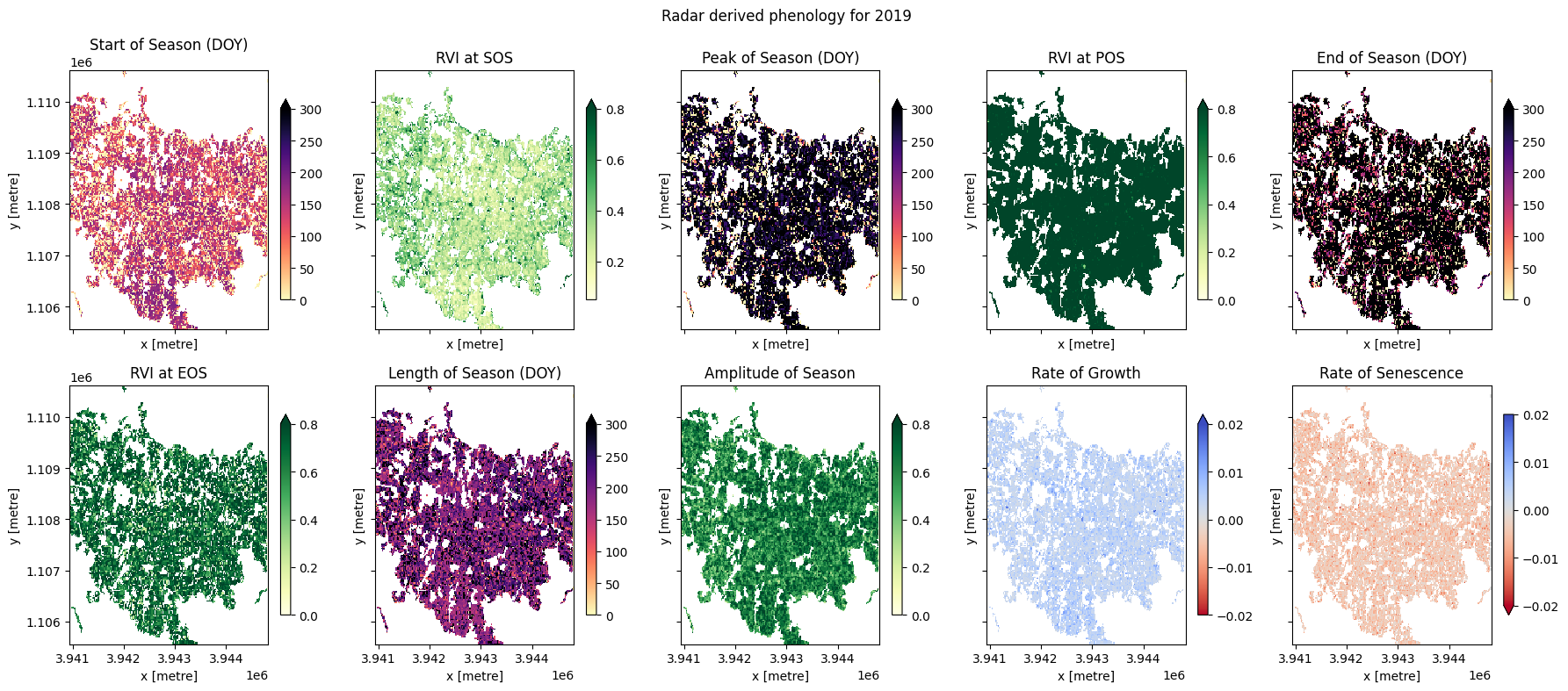
Per-pixel phenology statistics¶
We can now calculate the statistics for every pixel in our time-series and plot the results.
[18]:
# find all the years to assist with plotting
years = rvi_smooth.groupby("time.year")
# get list of years in ts to help with looping
years_int = [y[0] for y in years]
# store results in dict
pheno_results = {}
# loop through years and calculate phenology
for year in years_int:
# select year
da = dict(years)[year]
# calculate stats
stats = xr_phenology(
da,
method_sos=method_sos,
method_eos=method_eos,
stats=pheno_stats,
verbose=False,
)
# add results to dict
pheno_results[str(year)] = stats
The phenology statistics have been calculated seperately for every pixel in the image. Let’s plot each of them to see the results.
Below, pick a year from the phenology results to plot.
[19]:
# Pick a year to plot
year_to_plot = "2019"
At the top if the plotting code we re-mask the phenology results with the crop-mask. This is because xr_phenologyhas methods for handling pixels with only NaNs (such as those regions outside of the polygon mask), so the results can have phenology results for regions outside the mask. We will therefore have to mask the data again.
[20]:
# select the year to plot
phen = pheno_results[year_to_plot]
# mask again with crop-mask
phen = phen.where(cm == 1)
# set up figure
fig, ax = plt.subplots(nrows=2, ncols=5, figsize=(18, 8), sharex=True, sharey=True)
# set colorbar size
cbar_size = 0.7
# set aspect ratios
for a in fig.axes:
a.set_aspect("equal")
# start of season
phen.SOS.plot(
ax=ax[0, 0],
cmap="magma_r",
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[0, 0].set_title("Start of Season (DOY)")
phen.vSOS.plot(
ax=ax[0, 1], cmap="YlGn", vmax=0.8, cbar_kwargs=dict(shrink=cbar_size, label=None)
)
ax[0, 1].set_title("RVI at SOS")
# peak of season
phen.POS.plot(
ax=ax[0, 2],
cmap="magma_r",
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[0, 2].set_title("Peak of Season (DOY)")
phen.vPOS.plot(
ax=ax[0, 3], cmap="YlGn", vmax=0.8, cbar_kwargs=dict(shrink=cbar_size, label=None)
)
ax[0, 3].set_title("RVI at POS")
# end of season
phen.EOS.plot(
ax=ax[0, 4],
cmap="magma_r",
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[0, 4].set_title("End of Season (DOY)")
phen.vEOS.plot(
ax=ax[1, 0], cmap="YlGn", vmax=0.8, cbar_kwargs=dict(shrink=cbar_size, label=None)
)
ax[1, 0].set_title("RVI at EOS")
# Length of Season
phen.LOS.plot(
ax=ax[1, 1],
cmap="magma_r",
vmax=300,
vmin=0,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[1, 1].set_title("Length of Season (DOY)")
# Amplitude
phen.AOS.plot(
ax=ax[1, 2], cmap="YlGn", vmax=0.8, cbar_kwargs=dict(shrink=cbar_size, label=None)
)
ax[1, 2].set_title("Amplitude of Season")
# rate of growth
phen.ROG.plot(
ax=ax[1, 3],
cmap="coolwarm_r",
vmin=-0.02,
vmax=0.02,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[1, 3].set_title("Rate of Growth")
# rate of Sensescence
phen.ROS.plot(
ax=ax[1, 4],
cmap="coolwarm_r",
vmin=-0.02,
vmax=0.02,
cbar_kwargs=dict(shrink=cbar_size, label=None),
)
ax[1, 4].set_title("Rate of Senescence")
plt.suptitle("Radar derived phenology for " + year_to_plot)
plt.tight_layout();
Conclusions¶
In the example above, we can see most of the fields are following a similar cropping schedule and are therefore likely the same species of crop. We can also observe that some fields have not followed this schedule (e.g. the EOY plot shows some fields didn’t follow this schedule, probably because they either remained fallow during the year, or because there were two peaks during the year which may have confused the phenology stats). Differences in the rates of growth, and in the RVI values at different times of the season, may be attributable to differences in soil quality, watering intensity, or other farming practices.
Phenology statistics are a powerful way to summarise the seasonal cycle of a plant’s life. Per-pixel plots of phenology can help us understand the timing of vegetation growth and sensecence across large areas and across diverse plant species as every pixel is treated as an independent series of observations. This could be important, for example, if we wanted to assess how the growing seasons are shifting as the climate warms.
Additional information¶
License: The code in this notebook is licensed under the Apache License, Version 2.0. Digital Earth Africa data is licensed under the Creative Commons by Attribution 4.0 license.
Contact: If you need assistance, please post a question on the Open Data Cube Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here). If you would like to report an issue with this notebook, you can file one on
Github.
Compatible datacube version:
[21]:
print(datacube.__version__)
1.8.15
Last Tested:
[22]:
from datetime import datetime
datetime.today().strftime("%Y-%m-%d")
[22]:
'2023-09-19'