Modelling discharge at Mohembo using uppercatchment rainfall¶
Products used: ERA5
Description¶
The discharge data at Mohembo becomes much more sparse during the era of good quality satellite observations, making it unreliable for comparing discharge with surface water extent. This notebook will try to model the discharge at Mohembo using the upstream rainfall extracted from ERA5 in a previous notebook
Getting started¶
To run this analysis, run all the cells in the notebook, starting with the “Load packages” cell.
Load packages¶
Import Python packages that are used for the analysis.
[1]:
%matplotlib inline
import warnings
import datetime as dt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from deafrica_tools.spatial import xr_rasterize
from deafrica_tools.load_era5 import load_era5
[2]:
warnings.filterwarnings("ignore")
Analysis Parameters¶
[3]:
upstream_rainfall_1989_2009 = 'results/upstream_rainfall_daily_1989-01_to_2009-12.csv'
upstream_rainfall_2010_2021 = 'results/upstream_rainfall_daily_2010-01_to_2021-05-26.csv'
freq='Q-DEC'
max_lags = 3
sklearn_model = RandomForestRegressor
Retrieve historical rainfall data over all areas of interest¶
This data has already been retrieved from ERA5 so we can simply pull in the csv on disk
[4]:
upstream_rainfall_1989_2009 = pd.read_csv(upstream_rainfall_1989_2009, index_col='time',parse_dates=True)
upstream_rainfall_2010_2021 = pd.read_csv(upstream_rainfall_2010_2021, index_col='time',parse_dates=True)
rain = pd.concat([upstream_rainfall_1989_2009, upstream_rainfall_2010_2021])
No need to re-run this since the data has been saved in the results/ folder
[5]:
# # Original shapefile from https://data.apps.fao.org/map/catalog/srv/api/records/57bb1c95-2f00-4def-886f
# vector_file = 'data/OB_FWR_Hydrography_Okavango_Subasins_polygon.geojson'
# # define time period of interest
# time_range = '1989-01', '2009-12'
# # load basin polygons
# # Original shapefile from https://data.apps.fao.org/map/catalog/srv/api/records/57bb1c95-2f00-4def-886f-caee3d756da9
# basin = gpd.read_file(vector_file)
# # upstream include Cuito and Cubango subbasins
# upstream = basin[basin.Subbasin.isin(['Cuito', 'Cubango'])]
# print(upstream)
# # get historical rainfall for upstream and delta
# bounds = upstream.total_bounds
# lat = bounds[1], bounds[3]
# lon = bounds[0], bounds[2]
# # download ERA5 rainfall and aggregate to monthly
# var = 'precipitation_amount_1hour_Accumulation'
# precip = load_era5(var, lat, lon, time_range, reduce_func=np.sum, resample='1D').compute()
# # fix inconsistency in axis names
# precip = precip.rename({'lat':'latitude', 'lon':'longitude'})
# upstream_raster = xr_rasterize(upstream, precip, x_dim='longitude', y_dim='latitude')
# upstream_rainfall = precip[var].where(upstream_raster).sum(['latitude','longitude'])
# upstream_rainfall.to_dataframe().drop('spatial_ref',axis=1).rename({'precipitation_amount_1hour_Accumulation':'cumulative daily rainfall (mm)'},axis=1).to_csv(f'results/upstream_rainfall_daily_{time_range[0]}_to_{time_range[1]}.csv')
Import discharge data¶
[6]:
discharge = 'data/mohembo_daily_water_discharge_data.csv'
dis=pd.read_csv(discharge)
dis['date'] = pd.to_datetime(dis['date'], dayfirst=True)
dis = dis.set_index('date')
Match discharge with rainfall¶
[7]:
dis = dis.loc[(dis.index >= rain.index[0])]
[8]:
df = rain.join(dis, how='outer')
df.tail()
[8]:
| cumulative daily rainfall (mm) | water_discharge | |
|---|---|---|
| 2021-05-22 | 0.0 | 201.356 |
| 2021-05-23 | 0.0 | 202.850 |
| 2021-05-24 | 0.0 | 200.148 |
| 2021-05-25 | 0.0 | 192.258 |
| 2021-05-26 | 0.0 | 193.073 |
Resample seasonal or monthly cumulative totals¶
By intergrating rainfall over a longer time-period (months to seasons) we can better correlate cumulative upstream rainfall with discharge at Mohembo.
[9]:
#total rainfall per month
df = df.resample(freq).sum()
df.head()
[9]:
| cumulative daily rainfall (mm) | water_discharge | |
|---|---|---|
| 1989-03-31 | 114.574218 | 41274.290 |
| 1989-06-30 | 22.230042 | 38089.340 |
| 1989-09-30 | 0.119446 | 20520.900 |
| 1989-12-31 | 37.682495 | 11343.479 |
| 1990-03-31 | 137.858338 | 24604.860 |
Split dataset at 2010. That way we can build a model on the historical, complete dataset, and then predict on the incomplete record from 2010 onwards
[10]:
df_2010 = df.loc[(df.index >= pd.to_datetime('2010-01-01'))]
df_1989 = df.loc[(df.index < pd.to_datetime('2010-01-01'))]
df_1989.tail()
[10]:
| cumulative daily rainfall (mm) | water_discharge | |
|---|---|---|
| 2008-12-31 | 95.044922 | 12850.7990 |
| 2009-03-31 | 125.729308 | 45340.2135 |
| 2009-06-30 | 6.483582 | 49117.4010 |
| 2009-09-30 | 1.598633 | 18477.3465 |
| 2009-12-31 | 82.677734 | 13901.3405 |
Explore correlations with lags in rainfall¶
[11]:
def crosscorr(datay, datax, lag=0):
"""
Lag-N cross correlation.
lag : int, default 0
datax, datay : pandas.Series objects of equal length
"""
return datay.corr(datax.shift(lag))
[12]:
# calculate cross correlation for each lag period
xcov = [crosscorr(df_1989['water_discharge'], df_1989['cumulative daily rainfall (mm)'], lag=i) for i in range(max_lags)]
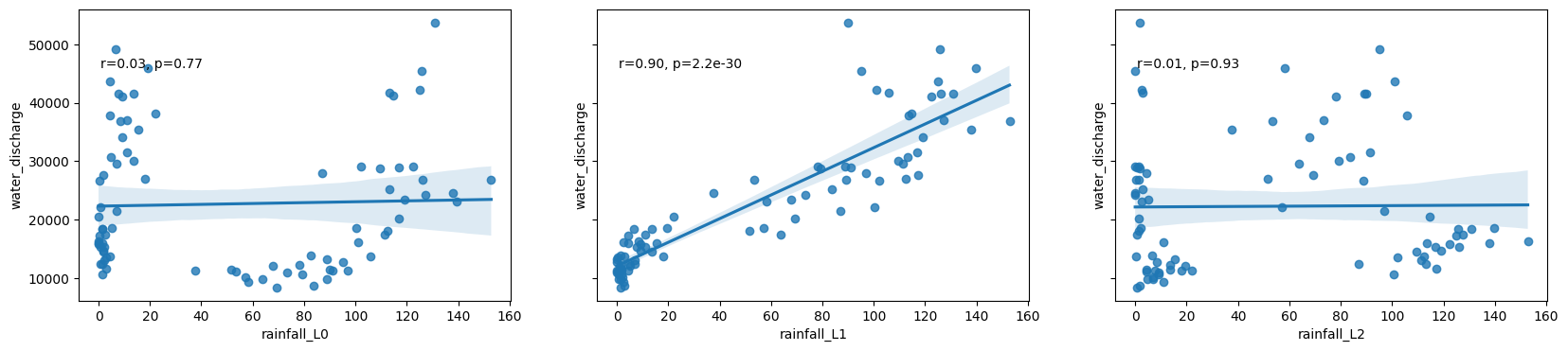
# Scatter plots of the relationship between rainfall and discharge at each lag
fig, ax = plt.subplots(1,max_lags, figsize=(20,4), sharey=True)
for lag in range(max_lags):
df_1989['rainfall_L'+str(lag)] = df_1989['cumulative daily rainfall (mm)'].shift(lag)
sns.regplot(x='rainfall_L'+str(lag), y='water_discharge', data=df_1989, ax=ax[lag])
r, p = stats.pearsonr(df_1989['rainfall_L'+str(lag)][lag:], df_1989['water_discharge'][lag:])
ax[lag].text(.05, .8, 'r={:.2f}, p={:.2g}'.format(r, p), transform=ax[lag].transAxes)
Regression modelling¶
Model the relationship between rainfall and discharge using the lag that corresponds with the highest correlation
Conduct a test/train split first to get an idea of the general accuracy of this approach
[13]:
max_value = max(xcov)
best_lag = xcov.index(max_value)
print("Best lag:",best_lag)
Best lag: 1
[14]:
#convert data into a format that scikit learn likes
X = df_1989['rainfall_L'+str(best_lag)][best_lag:].values.reshape(-1,1)
y = df_1989['water_discharge'][best_lag:].values.reshape(-1,1)
#conduct a train test split
X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1)
#model the relationship using just the training data, then predict on test data
model = sklearn_model()
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
print('MAE: ',mean_absolute_error(y_test,y_pred))
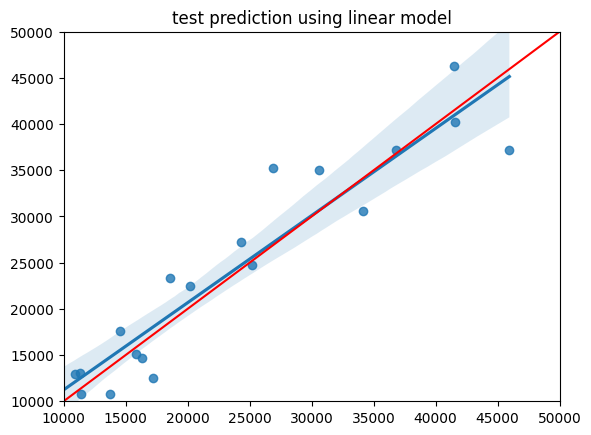
#plot result of test data
sns.regplot(x=y_test, y=y_pred)
plt.xlim(10000, 50000)
plt.ylim(10000, 50000)
plt.plot([10000, 50000], [10000, 50000], 'k-', color = 'r')
plt.title('test prediction using linear model');
MAE: 3267.4222390809487
Predict Discharge at Mohembo¶
Grab the rainfall from the period we want to predict
[15]:
fc_rainfall=df['cumulative daily rainfall (mm)'].shift(best_lag)
X_fc = fc_rainfall[best_lag:].values.reshape(-1,1)
Make a prediction using rainfall data
[16]:
# model = LinearRegression()
model = sklearn_model()
model.fit(X,y) #train 1989-2010
fc = model.predict(X_fc) # predict on all data
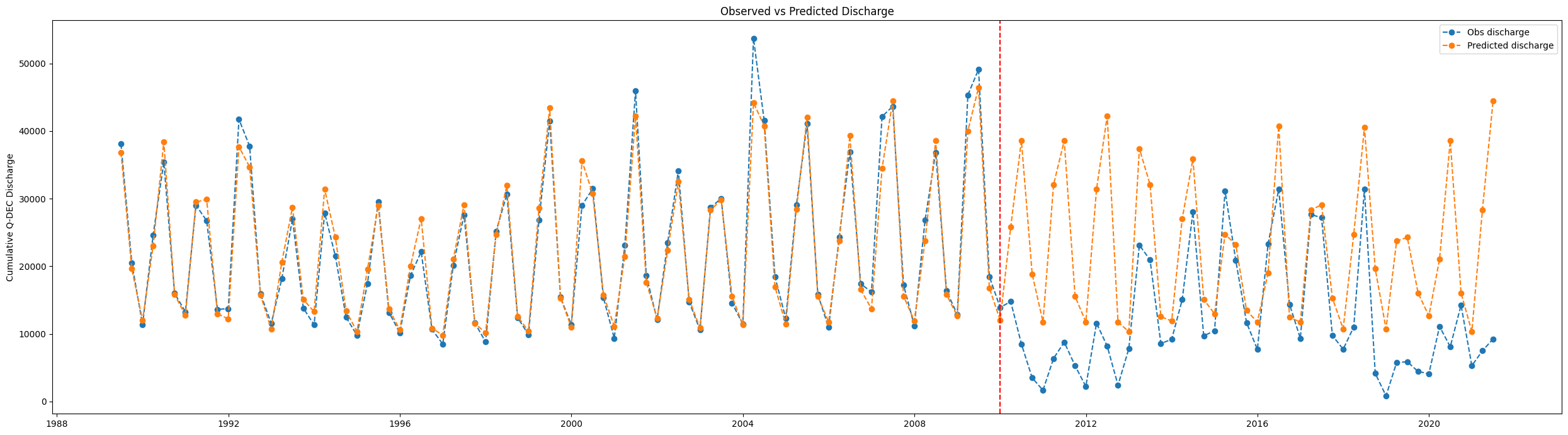
Plot the observed vs predicted discharge as a time series¶
[17]:
df_predicted = df[best_lag:]
df_predicted['predicted_discharge'] = fc.reshape(-1)
df_predicted.head(2)
[17]:
| cumulative daily rainfall (mm) | water_discharge | predicted_discharge | |
|---|---|---|---|
| 1989-06-30 | 22.230042 | 38089.34 | 36847.73170 |
| 1989-09-30 | 0.119446 | 20520.90 | 19623.61006 |
Print mean absolute error¶
[18]:
mean_absolute_error(df_predicted.loc[(df_predicted.index < pd.to_datetime('2010-01-01'))]['water_discharge'],
df_predicted.loc[(df_predicted.index < pd.to_datetime('2010-01-01'))]['predicted_discharge'])
[18]:
1562.6560681098642
[19]:
fig, ax = plt.subplots(figsize=(25,7))
ax.plot(df_predicted['water_discharge'], label='Obs discharge', linestyle='dashed', marker='o')
ax.plot(df_predicted['predicted_discharge'], label = 'Predicted discharge', linestyle='dashed', marker='o')
ax.legend()
plt.title('Observed vs Predicted Discharge')
ax.set_ylabel('Cumulative '+freq+' Discharge')
ax.axvline(dt.datetime(2010, 1, 1), c='red',linestyle='dashed')
ax.set_xlabel('')
plt.tight_layout();
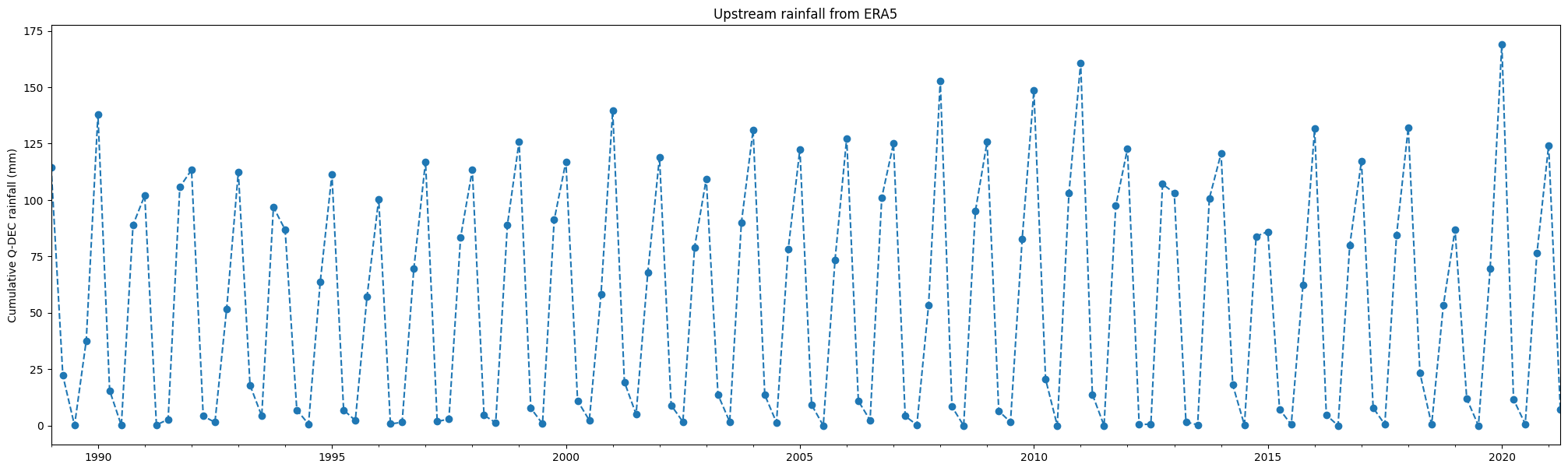
Plot rainfall¶
[20]:
df['cumulative daily rainfall (mm)'].plot(linestyle='dashed', marker='o',figsize=(25,7))
plt.title('Upstream rainfall from ERA5')
plt.ylabel('Cumulative '+freq+' rainfall (mm)')
plt.xlabel('');
[21]:
data = 'results/okavango_all_datasets.csv'
ok_r=pd.read_csv(data, index_col='time', parse_dates=True)[['okavango_rain']]
Save result to disk¶
[22]:
df_predicted.rename({'cumulative daily rainfall (mm)':'upstream_rainfall'}, axis=1).to_csv('results/modelled_discharge_'+freq+'.csv')
Additional information¶
License: The code in this notebook is licensed under the Apache License, Version 2.0. Digital Earth Africa data is licensed under the Creative Commons by Attribution 4.0 license.
Contact: If you need assistance, please post a question on the Open Data Cube Slack channel or on the GIS Stack Exchange using the open-data-cube tag (you can view previously asked questions here). If you would like to report an issue with this notebook, you can file one on
Github.
Last Tested:
[23]:
from datetime import datetime
datetime.today().strftime('%Y-%m-%d')
[23]:
'2023-08-21'